协方差的定义是什么

在概率论中，两个随机变量 X 与 Y 之间相互关系，大致有下列3种情况：

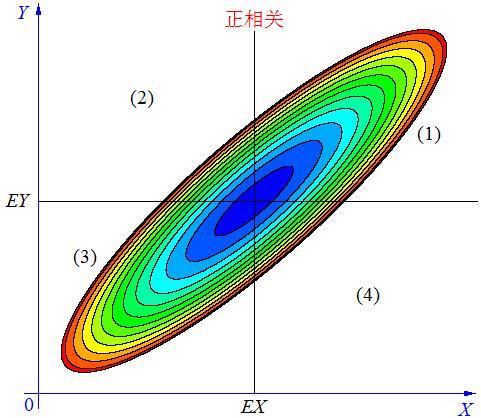
情况一,如上, 当 X, Y 的联合分布像上图那样时，我们可以看出，大致上有： X 越大 Y 也越大， X 越小 Y 也越小，这种情况，我们称为“正相关”。

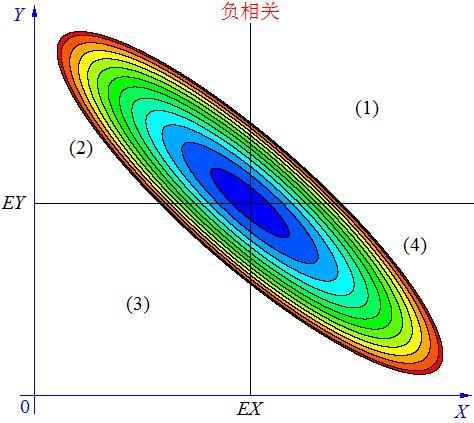
情况二, 如上图, 当X, Y 的联合分布像上图那样时，我们可以看出，大致上有：X 越大Y 反而越小，X 越小 Y 反而越大，这种情况，我们称为“负相关”。

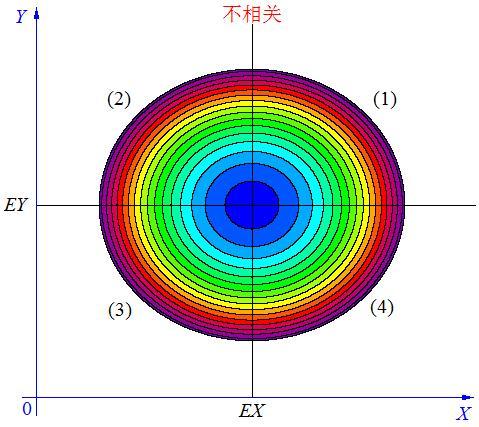
情况三,如上图, 当X, Y 的联合分布像上图那样时，我们可以看出：既不是X 越大Y 也越大，也不是 X 越大 Y 反而越小，这种情况我们称为“不相关”。

怎样将这3种相关情况，用一个简单的数字表达出来呢？

在图中的区域（1）中，有 X>EX ，Y-EY>0 ，所以(X-EX)(Y-EY)>0；

在图中的区域（2）中，有 X<EX ，Y-EY>0 ，所以(X-EX)(Y-EY)<0；

在图中的区域（3）中，有 X<EX ，Y-EY<0 ，所以(X-EX)(Y-EY)>0；

在图中的区域（4）中，有 X>EX ，Y-EY<0 ，所以(X-EX)(Y-EY)<0。

当X 与Y 正相关时，它们的分布大部分在区域（1）和（3）中，小部分在区域（2）和（4）中，所以平均来说，有E(X-EX)(Y-EY)>0 。

当 X与 Y负相关时，它们的分布大部分在区域（2）和（4）中，小部分在区域（1）和（3）中，所以平均来说，有(X-EX)(Y-EY)<0 。

当 X与 Y不相关时，它们在区域（1）和（3）中的分布，与在区域（2）和（4）中的分布几乎一样多，所以平均来说，有(X-EX)(Y-EY)=0 。

所以，我们可以定义一个表示X, Y 相互关系的数字特征，也就是

协方差

cov(X, Y) = E(X-EX)(Y-EY)

当 cov(X, Y)>0时，表明 X与Y 正相关；

当 cov(X, Y)<0时，表明X与Y负相关；

当 cov(X, Y)=0时，表明X与Y不相关。

这就是协方差的意义。

另外补充：

求特征协方差矩阵，如果数据是3维，那么协方差矩阵是

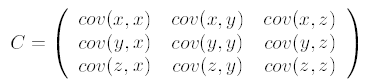
这里只有x和y，求解得

对角线上分别是x和y的方差，非对角线上是协方差。协方差大于0表示x和y若有一个增，另一个也增；小于0表示一个增，一个减；协方差为0时，两者独立。协方差绝对值越大，两者对彼此的影响越大，反之越小。